
Welcome to the Map Reading Guide, from TopoWeb. Whether you're just getting started with topographic maps, need to brush up on your skills, or are looking to learn something new, this page should help you.
A topographic map shows the elevation data for a certain part of the earth, in addition to other physical and man-made features. In the U.S., the United States Geological Survey (USGS) is the main distributor of topographic maps. The USGS creates several scales of maps. 7.5 minute maps (scale 1:24000) are the most detailed. All map samples shown below are from 7.5' maps.
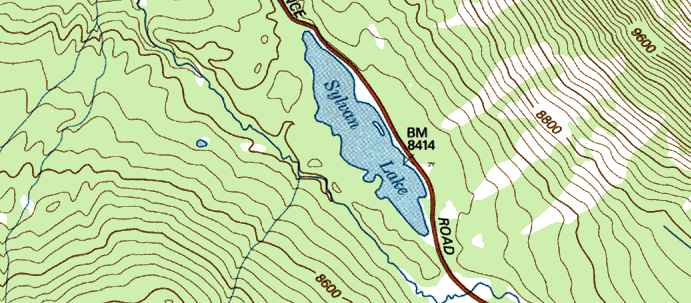
Above is a small part of a USGS map. 7.5 minute maps are so called because each covers 7.5 minutes of latitude and 7.5 minutes of longitude on the earth's surface. On the ground, this is approximately equal to eight miles (north and south) by six miles (east and west). Each 7.5' paper map (called a quadrangle, or just a quad) is about 28 inches long by 21 inches wide. They can be purchased from the USGS or from most outdoor shops. (Ordering Info).
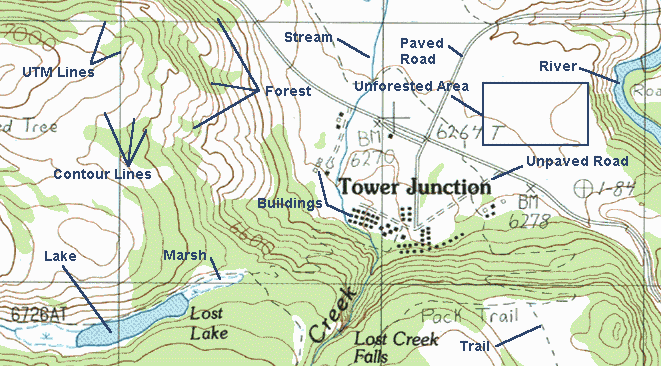
Before getting into contours, take a look at the map above. Topographic maps also show many cultural and physical features. Some of the more common map symbols are labeled. Here are explanations for the non-contour symbols shown above:
For a list of additional USGS map symbols, go the the USGS Symbol Page.
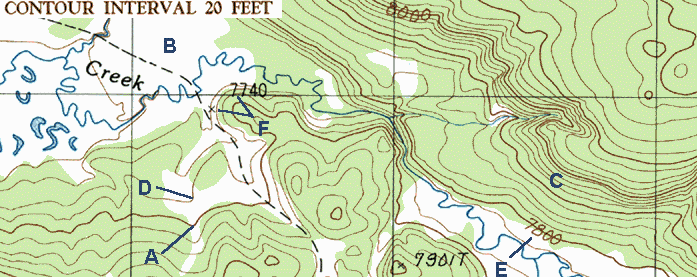
Contour lines are the continuous brown lines found on topographic maps that give information about elevation. Each line represents a specific elevation, and all locations along that line have the exact same elevation. For example, observe the line indicted by (A) in the map above. If you were to walk along that line on the ground, your elevation would never change.
Notice the words "Contour Interval 20 Feet", which are found along the bottom collar of USGS maps. This means that the elevation change between contour lines is 20 feet. The line at (D), for example, has an elevation that is 20 feet below that of (A). It follows, then, that a place on the map with many contour lines together has a large amount of elevation change-- a hillside. The area around (C) is a hillside. Likewise, places like (B) with few contour lines have little elevation change and are flat.
You may have noticed that every fifth contour line is darker than the others. The darker contour lines (like (A)) are called Index Contours. If you follow an index line, you will eventually find a place where the elevation of that line is given. (E) is an example of such a place. Another way to find elevations is to use Spot Elevations, like the one shown at (F). These consist of an 'X' next to a number. The number tells the elevation at the location marked by the X. The X indicated by (F) has an elevation of 7,740 feet. There is also another spot elevation on this map. It says '7901T'. Ignore the T, and the elevation there is 7,901 feet.
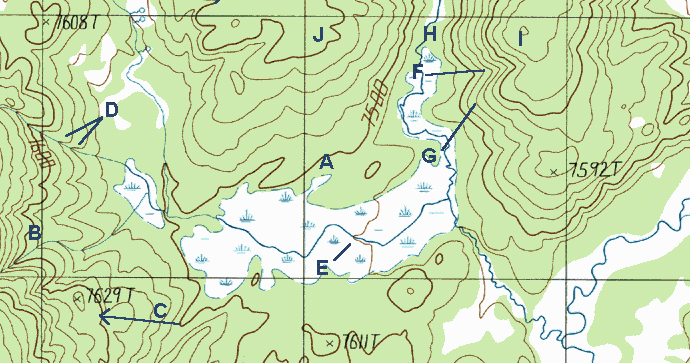
How can you tell which side of a hillside is the highest? There are several ways. For the first, look at contour lines (A) and (B) in the map above. Note that (A) is at 7500 ft. and (B) is at 7600 ft. Any line from (A) to (B), then, should be uphill. If you were to travel from east to west on line (C), for example, you would travel uphill. Since the difference between (A) and (B) is 100 feet, there would be exactly 100 vertical feet of elevation gain.
A quicker way to find elevation changes is to use creeks and streams. Since water travels downhill, finding the direction that a stream travels can quickly tell you about relief along the length of the watercourse. Fortunately, it is easy to do. Look at the stream indicated by (D) above. Notice that when contour lines run into this stream, they form a 'V' shape that appears to point to the left. On all streams, the V formed by contour lines always points upstream, and therefore uphill. This tells you that the highest point along that hillside is at the left side. Also, check the V shape at point (E). Even though the stream is in a relatively flat area, the upstream-pointing V is still visible.
What about the hillside between (H) and (I)? Most larger streams tend to flow at a low point between two high points-- in this case, (I) and (J). From point (H), then, you would be walking uphill if you went east or west. Also, a closed circle like the small one at (I) indicates a high point.
At point (F), you can see that the contour lines form V's that point uphill. This may be a dry or intermittent stream. The land shape indicated by uphill-pointing V's, whether or not there is a stream, is a small canyon or gully. (G) is similar, except the rounded V's appear to point downhill. On the ground, this looks like a promontory that extends outward.
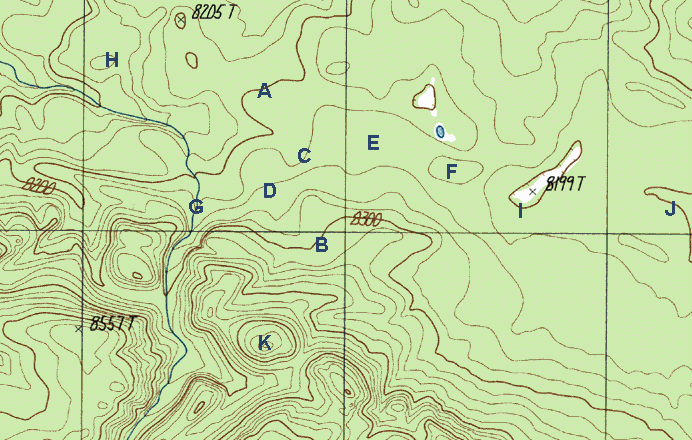
This map may look considerably more difficult to interpret, but don't panic. First, look at index contours (A) and (B). You can see that (A) is at 8200 feet and (B) is at 8300. Therefore, a walk from (A) to (B) would be uphill (you can examine the stream at (G) to confirm this). Now look at the line at (C). The contour interval for this map is 20 feet. This means that (C) has an elevation of 8220 feet, since it is one line uphill from (A). Line (D), then has an elevation of 8240 feet.
The elevation of areas between contour lines is simple enough to approximate. Location (E) is between the 8220 and 8240 contour lines, so its elevation is somewhere between those figures. But what about the contour line surrounding (F)? If you were to walk from (E) to (F), would you go uphill or downhill?
To answer that, it helps to know that every regular closed circular-shaped contour line is a high point. The contour circle at (H), for example, shows that the land inside it is higher than the surrounding land. Similiarly, (F) is a high point, and a walk from (E) to (F) would be uphill. The elevation of the contour line around (F) is actually 8240, the same as at (D). If you were to walk between (D) and (F), your elevation would drop somewhat, then increase as you crossed the 8240 contour again. Concentric circles, such as those found around (K), always have a high point at their center.
There is one exception to the above rule about closed contours being high points. Note the index contour at (I). There are tiny tick marks pointing to the inside of the shape. This is a depression with no outlet. The contour line is at 8200 feet, and everything inside it is less than 8200 feet. Contour lines (I) and (J) are both at the same elevation. If you were to walk from (J) to (I), you would climb slightly above 8200 feet before dropping into the depression (8199 feet).
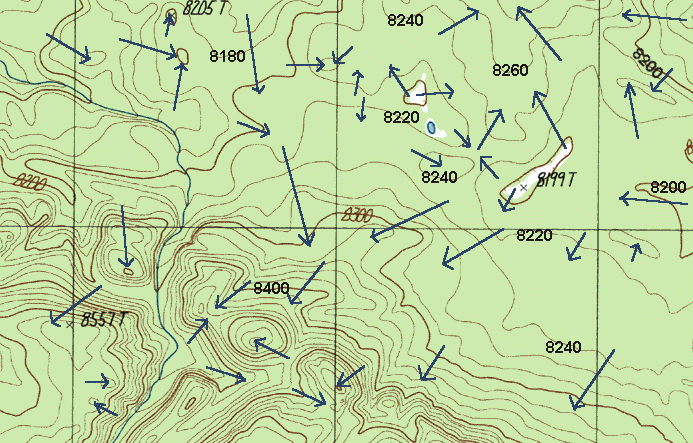
If you had some trouble with some of the tougher spots on the previous map, check this one out. It has many of the crucial non-index contours marked. In addition, all the arrows on it point from lower places to higher places. This should help you to better understand contour lines. And if you can read this topographic map, you can read just about any one.
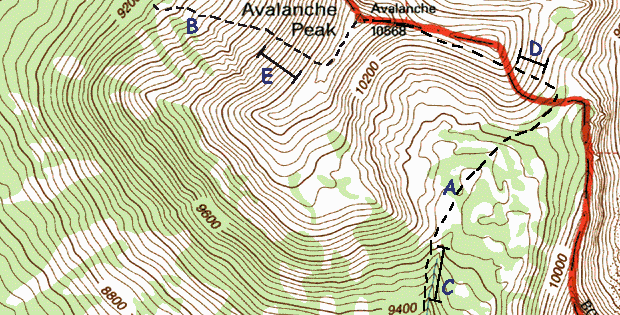
This is a nifty trick that is especially useful for hikers who like to go cross-country and climb mountains. You can also use it to find out how steep, on average, a trail will be. Take a look at the map above. In real life, Avalanche Peak has a trail to the summit. But we'll pretend it doesn't. You want to reach the top, and you're considering two routes, (A) and (B). (A) has two separate parts that are steep, while (B) has one long, steep section.
First, select a section to measure. Try to pick the steepest segment of the climb, and one that has uniform contour lines between two points. Then measure the ground distance using a ruler and scale (for paper maps) or software (for digital maps). In this example, segment (C) turns out to be 730 feet in length (on the ground). Then determine vertical rise, using the contour lines. Here, the interval is 40 feet, for a total rise of 200 feet.
Now that you have Rise (elevation change) and Run (length), calculating grade is easy with a calculator. The formula is (Rise/Run)*100. In this case, it would be (200/730)*100 = 27.4% gradient. You can use this technique on places you have been to determine what the grade for a steep trail is, or for a climbable scree slope.
Gradient is simply a measure of feet of rise per 100 feet of run. I prefer to get an actual measure of a route's slope in degrees from the horizontal. Unfortunately, it requires a bit of trigonometry. The formula is arctan(rise/run). You can do this using the Windows calculator by turning it to Scientific mode. First, check 'Inv' on. Divide the Rise by the Run, then select 'tan'. This is the slope's angle in degrees. It may seem surprisingly small, but keep in mind that 15 degrees is a very steep trail and 30 degrees is a steep mountain slope.
Back to the example. It turns out that (C) is a 15 degree slope, (D) is 30 degrees, and (E) is 36 degrees. Both (D) and (E) would be steep, tough climbs, but (D) might be the better choice. Good luck using this method. I hope you can plan many fun trips using it.
Thank you for looking at this page. I hope it has helped you to read topographic maps better. All examples on this page are from different locations in Yellowstone National Park. If you have questions, comments, or suggestions about this page or topographic maps, feel free to contact me at [email protected]. All text and illustrations on this page were created by me (Doug Armknecht). If you're interested in seeing where topo maps can take you, take a look at my trip reports from the 500 Miles in Yellowstone that I hiked and backpacked during the summers of 1998 and 1999.
